 The Binomial distribution is a discrete probability distribution closely related to the Bernoulli Distribution. Here, I will present the binomial distribution from a SAS point of view by code example. It models the number of successes in a series of
The Binomial distribution is a discrete probability distribution closely related to the Bernoulli Distribution. Here, I will present the binomial distribution from a SAS point of view by code example. It models the number of successes in a series of ![]() independent Bernoulli trials. Furthermore, if
independent Bernoulli trials. Furthermore, if ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If a stochastic variable ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Binomial Distribution SAS Code Example
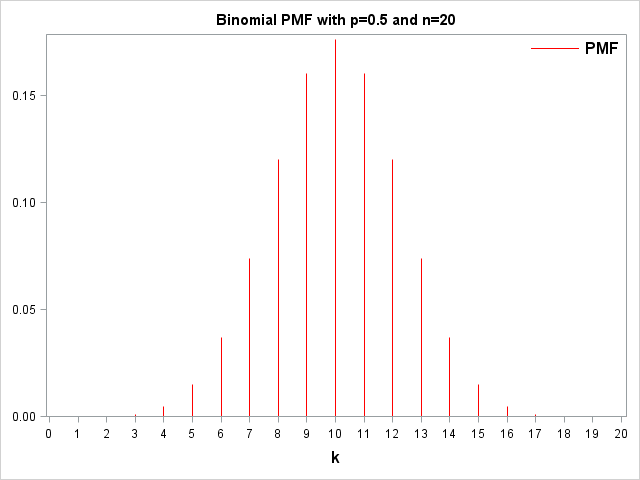
Let us plot the Probability Mass Function. First of all, I create the PMF data, specifying the probability of success in the individual Bernoulli trials and the number of trials to be performed. Then I use the PDF function to calculate the PMF values. Finally, I use a needle plot to create the graph to the right if the Probability Mass Function.
/* Generate PMF Data */ %let p=0.5; %let n=20; data Bino_PMF; do k=0 to &n; PMF=pdf('Binomial', k, &p, &n); output; end; run; /* Plot PMF */ title "Binomial PMF with p=&p and n=&n"; proc sgplot data=Bino_PMF noautolegend; needle x=k y=PMF / lineattrs=(color=red); xaxis values=(0 to 20) label='k' labelattrs=(size=12 weight=Bold); yaxis display=(nolabel); keylegend / position=NE location=inside across=1 noborder valueattrs=(Size=12 Weight=Bold); run; title; |
Finally, this distribution is one of the first distributions you will meet in your statistics class. Therefore, I encourage you to play around with the ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For other distributions, see the Exponential Distribution and the F Distribution.
In addition, You can download the entire program supporting this example here.
