 The Bernoulli distribution is probably the simplest of the common, discrete distributions. It has only two outcomes,
The Bernoulli distribution is probably the simplest of the common, discrete distributions. It has only two outcomes, ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
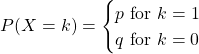
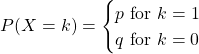
The Bernoulli distribution is a special case of the Binomial Distribution, which models the number successes in a series of Binomial trials. In a Bernoulli trial, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bernoulli Distribution SAS Code Example
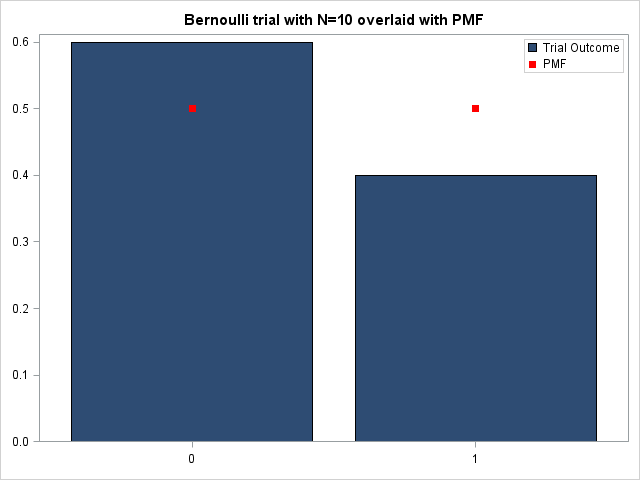
Lets us look at a small example of a Bernoulli trial. Suppose we toss a fair coin 10 times and record the number of heads and tails of the outcome. We define heads as “Success” and tails as “Failure, though reversing this definition will make no difference. Below, I have written the SAS code to perform this trial.
%let p=.5; %let N=10; data Bernoulli_Trial; call streaminit(555); do i=1 to &N; x=rand('Bernoulli', &p); output; end; run; |
If you are not at all familiar with the Bernoulli, watch this basic introduction at Khan Academy. Another natural extension to the Bernoulli distribution in SAS is the Table Distribution. The Table distribution lets you sample from more than two outcomes and specify the associated probabilities. Basically, this is a Bernoulli with more than two outcomes. This is a very important extension and I encourage you to get to know it.
You can download the entire code with the Bernoulli trial here.
