When we work with large data sets in SAS, it is crucial to be able to draw subsets efficiently. In the blog post Using Indexes to Increase Performance in SAS, I demonstrate how to use an index to quickly draw small subsets of large data sets. While an index may be the obvious choice, there are alternatives. The SAS Hash Object Lookup Technique offers another approach to efficient subsetting of data. In this post, I discuss the differences between the two search approaches. Furthermore, I do a case study and look at performance for the two techniques.
The Index Search
When we use an index to find a key value, SAS uses a binary search algorithm. The binary search algorithm starts with the middle value. If the desired value is smaller, SAS focuses on the lower half of the ordered data. This process continues until the desired value is found or until it is concluded not to be present in the data. The binary search algorithm is a simple and effective way to search for data in large structures. Let us assume that we have an ordered table with N unique arbitrary keys. When N doubles, the maximum number of comparisons required to find or reject the presence of the key value of interest increases by 1. A more correct way to write it is that an ordered table with N unique arbitrary keys can be searched with O(log2(N)) comparisons. In contrast, if we do not use an index, but rely on sequential data step logic, the number of comparisons would double when the number of observations double. This means that the binary search scales much better when the number of observations increases.
The Hash Object Search
While the index algorithm can be very effective, it still has a few shortcomings. First of all, the table has to be sorted by the key value. This can be a very computational heavy process. Also, search time still does increases with the number of observations. SAS concurs both of them with the hash object search algorithm. The hash object algorithm starts with using a Hash Function on the key value. This hash function places the key in a search tree. The number of search trees (or AVL trees) is determined by the HASHEXP argument. The hash function is designed so that an almost equal number of keys are placed in each search tree. Next, when a search is performed for some key, the hash function is once again run on the key to be searched for. Then SAS focuses on the relevant AVL tree. Finally, a binary search is performed only in the tree. This means that the number of comparisons required to locate the key value is almost always reduced because SAS does not use the binary algorithm on the whole table but only a small part of it.
A case Study: Binary Search Vs Hash Object Algorithm
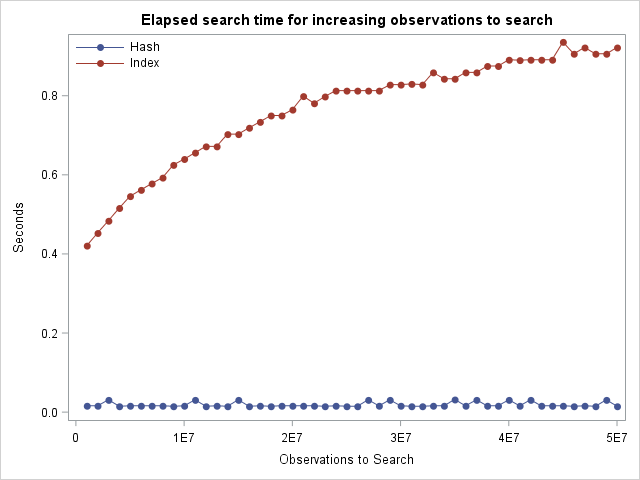
To demonstrate the points above, let us look at an example. In the code below, I do several runs of the same code with Call Execute Logic but with an increasing number of observations. I start with 200.000 observations of a made-up SAS data set. Then I use Proc Datasets to create a simple index on the variable ID. Finally, I perform 1000 hash searches and 1000 index searches. I save the elapsed time for the searches in a master data set for later analysis.
NB: The program takes about an hour to run on my system. If you want to test yourself, make sure to close all other programs and let the code run uninterrupted. This produces the most reliable results.
If you to not want to spend the full hour, change the upper limit of observations to 50e6 eg. The point will be intact, though not as clear.
The SAS Code
data MasterHashVsIndex; length ID $6 first_name $20 last_name $20 method $20 elapsedtime 8 nobs 8; run; data callstack; length string $5000; do obs=20e5 to 10e7 by 20e5; string=compbl(cats( " data MyData(drop=i); length ID $6 first_name $20 last_name $20; array first_names{20}$20 _temporary_ ('Paul', 'Allan', 'Bob', 'Michael', 'Chris', 'David', 'John', 'Jerry', 'James', 'Robert', 'Karen', 'Betty', 'Helen', 'Sandra', 'Sharon', 'Laura', 'Michelle', 'Angela', 'Melissa', 'Amanda'); array last_names{20}$20 _temporary_ ('Smith', 'Johnson', 'Williams', 'Jones', 'Brown', 'Miller', 'Wilson', 'Moore', 'Taylor', 'Hall', 'Anderson', 'Jackson', 'White', 'Harris', 'Martin', 'Thompson', 'Robinson', 'Lewis', 'Walker', 'Allen'); call streaminit(123); do i=1 to (", obs,"); ID=uuidgen(); first_name=first_names[ceil(rand('Uniform')*20)]; last_name=last_names[ceil(rand('Uniform')*20)]; output; end; run; proc datasets library=hash nolist; modify MyData; index delete _all_; index create ID / nomiss; run;quit; data HashvsIndex", obs, "(drop=rc i start); length ID $6 first_name $20 last_name $20 method $20; declare hash h(dataset:'MyData', hashexp:0); h.definekey('ID'); h.definedata(all:'Y'); h.definedone(); method='Hash'; nobs=", obs, "; start=time(); do i=1 to 10e3; ID=uuidgen(); rc=h.find(key:ID); end; elapsedtime=time()-start; put +10 '############################## ' elapsedtime ' ##############################'; output; method='Index'; nobs=", obs, "; start=time(); do i=1 to 10e3; ID=uuidgen(); set MyData key=ID; _ERROR_=0; end; elapsedtime=time()-start; put +10 '############################## ' elapsedtime ' ##############################'; output; stop; run; proc append base=MasterHashVsIndex data=HashvsIndex", obs, "; run;quit; proc datasets lib=hash nolist; delete HashvsIndex", obs, "; run;quit; " )); output; call execute(string); end; run; |
 I have plotted the elapsed time values above the code. The results are as expected from the theory behind the two algorithms. Both are reasonably fast. The hash search, however, is faster because it requires fewer comparisons by construction. Also, we see that when observations increase, run time increases for the index search. However, for the hash search, the elapsed time is constant because of the hash function and AVL tree structure.
I have plotted the elapsed time values above the code. The results are as expected from the theory behind the two algorithms. Both are reasonably fast. The hash search, however, is faster because it requires fewer comparisons by construction. Also, we see that when observations increase, run time increases for the index search. However, for the hash search, the elapsed time is constant because of the hash function and AVL tree structure.
Discussion
So if the hash search is faster and scales better, why even bother using an index search? Because the hash search is limited by memory and the SAS index is not. The SAS index is stored in a separate file, which is read when the index is used. Consequently, the index can handle much larger sizes of data than the hash object.
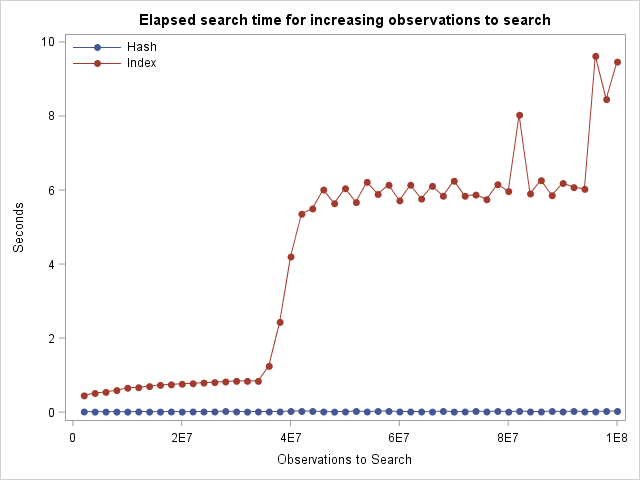
Since the index is stored on disk, an interesting thing happens when we upscale the number of rows even further (to 1 billion) in the code above. Consequently, the index file size increases as well. This means that SAS has to read the index in more than one turn due to I/O restrictions and the run time for the very large file size increases drastically as the plot to the right reveals.
The code to plot the run time data is below.
title "Elapsed search time"; proc sgplot data=MasterHashVsIndex; where elapsedtime ne .; series x=nobs y=elapsedtime / markers group=method markerattrs=(symbol=circlefilled); xaxis label="Observations to Search"; yaxis display=(nolabel); keylegend / position=nw location=inside across=1 noborder title=""; format nobs e10.; run; title; |
Summary
This post compared the different search algorithms used by the SAS index and SAS hash object. There are pros and cons to both approaches. However, we saw that the hash object is generally faster and scales much better than the index search. The only major drawback of the hash object search is that it is limited by available memory. The index is not, since SAS stores it on disk.
I have previously written several index and hash object related posts. Here are a few
The Importance Of SAS Index Centiles
Group Variable Values With The SAS Hash Object
SAS Hash Object DO_OVER Example
You can download the entire program from this post here.
