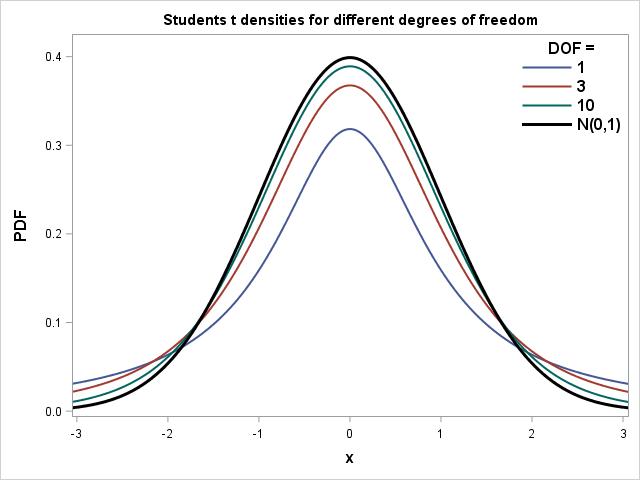
 The Student’s t distribution is a continuous probability distribution closely related to the Normal Distribution, defined in terms of the degrees of freedom associated with it. It models the distribution of a sample drawn from a standard normal distribution. It is widely used in many different fields of statistics. Examples include the construction of confidence intervals, assessment of statistical difference between two sample means and Linear Regression Analysis. Also, see the post One Sample T Test In SAS.
The Student’s t distribution is a continuous probability distribution closely related to the Normal Distribution, defined in terms of the degrees of freedom associated with it. It models the distribution of a sample drawn from a standard normal distribution. It is widely used in many different fields of statistics. Examples include the construction of confidence intervals, assessment of statistical difference between two sample means and Linear Regression Analysis. Also, see the post One Sample T Test In SAS.
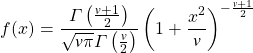
where ![]() is the degrees of freedom and
is the degrees of freedom and ![]() is the Gamme function. To the right, I have plotted Probability Density Functions for three t distributions with degrees of freedom equal to 1, 3 and 8 respectively. You can see that as the degrees of freedom increase, the tails of the distributions gets lighter and the distribution approaches the standard normal. A t distribution with
is the Gamme function. To the right, I have plotted Probability Density Functions for three t distributions with degrees of freedom equal to 1, 3 and 8 respectively. You can see that as the degrees of freedom increase, the tails of the distributions gets lighter and the distribution approaches the standard normal. A t distribution with ![]() is asymptotically equal to the standard normal distribution. You can download the SAS code, creating the plot here. For a more thorough introduction to the Student t distribution watch this video by JbStatistics.
is asymptotically equal to the standard normal distribution. You can download the SAS code, creating the plot here. For a more thorough introduction to the Student t distribution watch this video by JbStatistics.
Students t Code Example
Below, I have written a simple SAS code example. I encourage you to copy/paste this code into your editor and play around with the DOF macro variable setting the degrees of freedom in the t distribution. Familiarize yourself with how the shape of the Students t Probability Density Function changes with the degrees of freedom and how it approaches the standard normal for large values of ![]() .
.
/* Create Students t PDF data */ %let DOF=3; /* Degrees of Freedom */ data t_pdf; do x=-4 to 4 by 0.01; pdf_t = pdf('t', x, &DOF); /* PDF */ output; end; pdf_t = .; do x=-4 to 4 by 0.01; pdf_Normal = pdf('Normal', x); /* PDF for Standard Normal */ output; end; run; /* Draw Students t density and Standard Normal density */ title "Students t PDF with &DOF degrees of freedom and Standard Normal density"; proc sgplot data=t_pdf noautolegend; series x=x y=pdf_Normal / lineattrs=(thickness=3 color=black) legendlabel="N(0, 1)"; series x=x y=pdf_t / lineattrs=(color=red) legendlabel="t(&DOF)"; keylegend / location=inside position=NE across=1 noborder valueattrs=(Size=12 Weight=Bold);; yaxis display=(nolabel); xaxis min=-3 max=3 label='x' labelattrs=(size=12 weight=Boeld); run; title; |
