![]()
However, often you will see the density defined as
![]()
where ![]() .
. ![]() is the scale parameter and
is the scale parameter and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The Exponential is a special case of the Gamma distribution with shape parameter ![]()
![]()
![]()
![]()
![]()
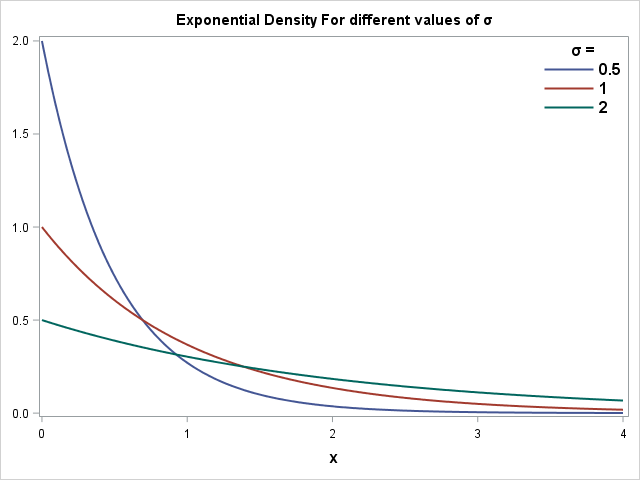
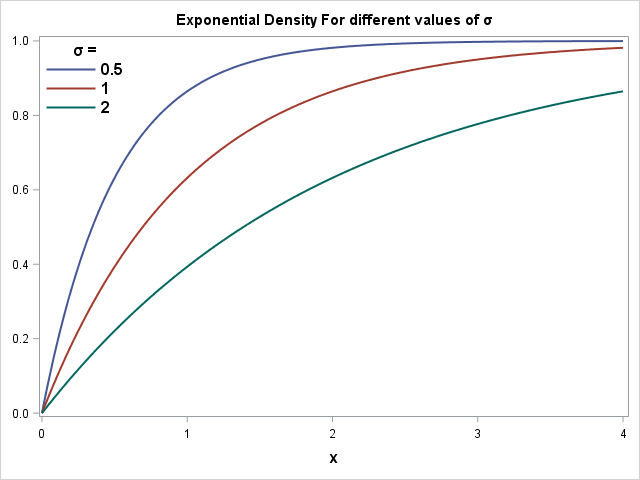
I plot the Probability Density Functions and the corresponding Cumulative Density Functions to the right. Here, I use different values of ![]()
![]()
![]()
![]()
![]()
![]()


SAS Code Example
The SAS code below lets you set ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
/* Exponential PDF Curves */ %let sigma = 1; data Exponential_PDF; do x=0 to 4 by 0.01; Exponential_PDF = pdf('Exponential', x, &sigma); output; end; run; /* Draw PDF Curve */ title "Exponential Density For (*ESC*){unicode sigma} = &sigma"; proc sgplot data=Exponential_PDF noautolegend; series x=x y=Exponential_PDF / lineattrs = (thickness=2 color=black) legendlabel="Exponential PDF"; keylegend / position=NE location=inside across=1 noborder valueattrs=(Size=12 Weight=Bold) titleattrs = (Size=12 Weight=Bold); xaxis label='x' labelattrs = (size=12 weight=Bold); yaxis display=(nolabel) label='PDF' labelattrs = (size=12 weight=Bold); run; title; |
Finally, check out the related pages about the Lognormal and Gamma Distribution in SAS.
