SAS Normal Distribution Code Example

The normal is the most common probability distribution. It is a continuous distribution and widely used in statistics and many other related fields. Therefore, it is a good idea to know the normal well. First, I will give a brief introduction. Then, I will show some code examples of the normal in SAS. The Probability Density Function is given as

$\begin{equation*} f(x\;|\;\mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}} \end{equation*}$

where $\mu$ is the mean and $\sigma^2$ is the variance and squared standard deviation. A random variable $X$ can follow a normal distribution with mean $\mu$ and standard deviation $\sigma$ . We write this as $X \sim \mathcal{N}(\mu,\,\sigma^{2})\,$ .

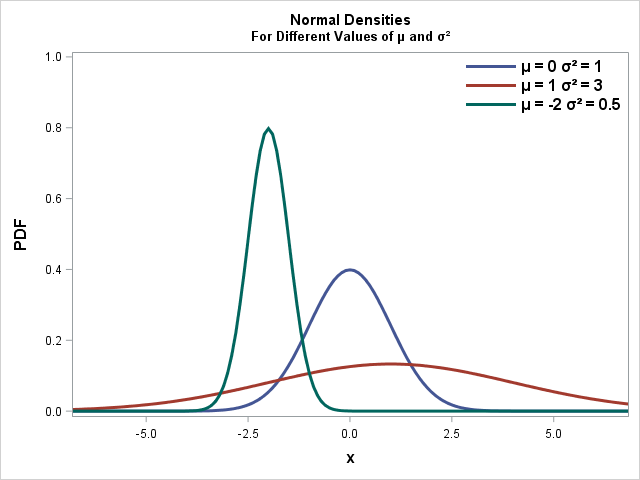
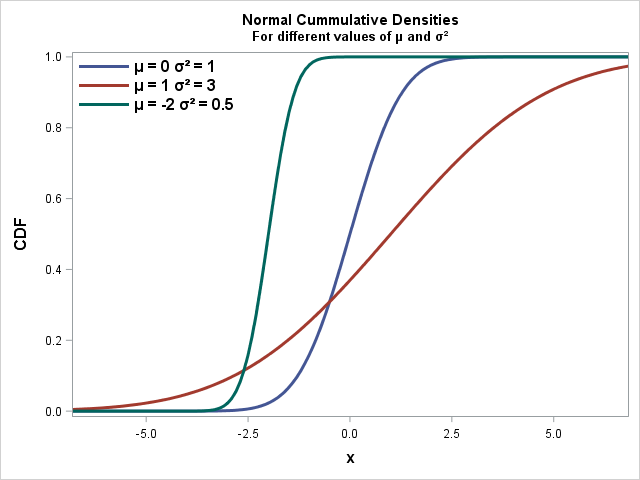
To the right, I plot the Probability Density Function (PDF) and the Cumulative Density Function (CDF) for three different normally distributed curves with different values of $\mu$ and $\sigma$ . The blue line is called the Standard Normal or Standard Gaussian with $\mu = 1$ and $\sigma^2 = 1$ . You can see that increasing $\sigma^2$ makes the distribution flatter, and decreasing $\sigma^2$ makes it steeper around the mean $\mu$ , which is the highest point on the density curve. You can download the entire program creating these plots here.

We use the normal in many different areas in statistics. A typical use of it is to assume normality, compute some test statistic and then evaluate this test statistic in the normal distribution to see if you can reject or fail to reject your null hypothesis. See the post Linear Regression in SAS for an example. Also, we use the normal distribution in the post Black Scholes Price in SAS.

SAS Code Example Normal Distribution Probability Density Function PDF

SAS Code Example Normal Distribution Commulative Density Function CDF

The Central Limit Theorem

The Normal Distribution is popular because of the Central Limit Theorem. It is considered to be one of the most fundamental and profound concepts in statistics. The central limit theorem states that even though we draw samples from some non-normal distribution, the sampling distribution of the mean will tend to normality as the sample size increases. For a basic introduction to the Central Limit Theorem, I recommend this Introduction to the Central Limit Theorem by Khan Academy. Previously, I have written a blog post about how to Visualize the Central Limit Theorem in SAS.

Normal Distribution SAS Code Example

It is important to have a basic understanding of the normal distribution. Also, you should know how the shape changes with its parameters. Below, I write SAS code example for you to play around with. Insert it into your SAS editor and change the three values defined at the top of the code.

%let alpha = 0.05; /* Set alpha value */
%let mu = 0;	   /* Set mean value */
%let sigma = 1;	   /* Set st. dev value */
 
data normal_PDF(drop = lower_q upper_q);
   lower_q = quantile('normal', &alpha/2 , &mu, &sigma);	            /* Set lower quantile         */
   upper_q = quantile('normal', (1 - &alpha/2), &mu, &sigma);	            /* Set upper quantile         */
 
   do x=&mu - 3*&sigma to &mu + 3*&sigma by 0.01;
      density = pdf('normal',x,&mu,&sigma);                                 /* Normal Density Function    */
      output;
   end;
   x = .; density = .;
 
   x_line = upper_q; line = pdf('normal',x_line,&mu,&sigma);output;         /* Line for upper quantile    */
   x_line = lower_q; line = pdf('normal',x_line,&mu,&sigma);output;         /* Line for lower quantile    */
   x_line = .; line = .;   
 
   do lower_x_band = &mu - 3*&sigma to lower_q by 0.01;                     
      lower_band = pdf('normal',lower_x_band,&mu,&sigma);                   /* Lower critical region      */                
      output;
   end;
   lower_x_band = .; lower_band = .;
 
   do upper_x_band = upper_q to &mu + 3*&sigma by 0.01;
      upper_band = pdf('normal',upper_x_band,&mu,&sigma);                   /* Lower critical region      */    
      output;
   end;
   upper_x_band = .; upper_band = .;
run;
 
title 'Normal Probability Density Function';
title2 'With Critical Regions Shaded';
proc sgplot data = normal_PDF noautolegend;
   series x = x y = density	/ lineattrs = (color = black thickness = 2);
   dropline x = x_line y = line / lineattrs = (color = black);
   band x = lower_x_band upper = lower_band lower = 0;
   band x = upper_x_band upper = upper_band lower = 0;
   yaxis offsetmin=0 min=0 label="Density";
   xaxis label = 'x';
run;
title;

Finally check out the blog post Fit Normal, Weibull and Lognormal Distribution to see how to fit the normal in SAS. For related distributions, see the Chi-Square.